O(N) to O(1)

This blog post is based on an interview question. I have changed the question to make it more generic.

🧠 Problem: What is the least number of digits needed from 1 to N to sum to K?

Example 1:
N = 5, K = 8

Answer: 2
Explanation: 

1, 2, 3, 4, 5

5 + 3 = 8

Example 2:
N = 3, K = 6

Answer = 3
Explanation:

1, 2, 3

1 + 2 + 3 = 6

When I first saw this question, my first instincts were to write a loop from \(N\) to 1 and to check each number and decide whether to add it or not. Since we would like to find the smallest subset from 1 to \(N\) such that it adds to \(K\), it makes sense to start from the largest number and work our way down.

“Premature optimisation is the root of all evil” - Donald Knuth

so lets just write out a simple working solution and worry about optimising later.

All code blocks are in pseudocode…

Linear-time Solution

Regardless of the complexity of the solution, we should always think about the edge cases and handle them first.

case 1: if sum(1..\(N\)) < \(K\) then no solution exists. We can use arithmetic progression for this to save time and space

function sum_1_N(N):
	return N*(N+1)/2

if sum_1_N(N) < K:
	return -1

case 2: ensure N, K ≥ 1

if N < 1 or K < 1:
	return -1

With that out of the way, lets write the main chunk of the code

function solution(N, K):

	//edge cases
	...
	//edge cases

	count = 0
	
	// if K <= N, then K is already available in the set from 1 to N
	if K <= N:
		return 1
	
	
	for i from N to 1:
		if i<=K:
			K = K - i
			count = count + 1
	return count

Going past O(n)

In order to see how to further optimise this, we should try out several examples and see if we can identify any patterns.

Example:
N = 5, K = 10

Answer = 3

1, 2, 3, 4, 5

5 + 4 + 1 = 10

Example:
N = 5, K = 11

Answer = 3

1, 2, 3, 4, 5

5 + 4 + 2 = 11

Example:
N = 6, K = 14

Answer = 3

1, 2, 3, 4, 5, 6

6 + 5 + 3 = 14

What we can learn from doing more and more examples like this is that we try to take from the back (largest numbers first) as much as possible (contiguously) then we are guaranteed that the remaining number exists in the rest of the number in the set.

Explanation (N = 6, K = 14):

1. First we start with i = 6. 6 is less than K so we take it. K now becomes 8.
2. Next we have i = 5. 5 is less than K (K = 8) so we take it. K now becomes 3.
3. Next we have i = 4. But 4 is greater than K (K = 3) so we cannot take it. 
	 However, if we consider the set of integers from 1 to i (i = 4), we know that
   3 exists in that set.

With this knowledge we can first make one optimisation - that is to iterate through the numbers from the back for as long as \(i\) ≥ \(K\) then if \(K\) is not 0, we can just add 1 to the count. This helps us stop iterating through the list earlier.

Lets start optimizing

How do we find the point at which we can no longer contiguously take from the back without iterating through the list? If we can find a way to find that point, then we can do a simple subtraction from \(N\) to find how many numbers to count.

Essentially, we are trying to find the sum of some \(m\) contiguous numbers from \(N\) that has a some that is close to \(K\). Lets write out the equation for the sum of contiguous number from \(a\) to \(b\), but \(b\) refers to \(N\) and \(a\) refers to the starting point (of the contiguous set of numbers)

Technically, \(a\) and \(N\) are meant to be integers but we are going to bend that rule for a second. Since we know that the sum from \(a\) to \(N\) is close to \(K\), lets form an equation using that and solve for \(a\)!

Now we have a quadratic in \(a\). Lets use the good old fashioned way to find the roots.

a = -1
b = 1
c = n**2 + n - 2*k
discriminant = b**2 - 4*a*c

There will be two roots, but we are only interested in the positive root.

pos_root = (-b - sqrt(discriminant))/2*a

Here is a plot from wolfram alpha to see what is going on (\(N\) = 6, \(K\) = 14):

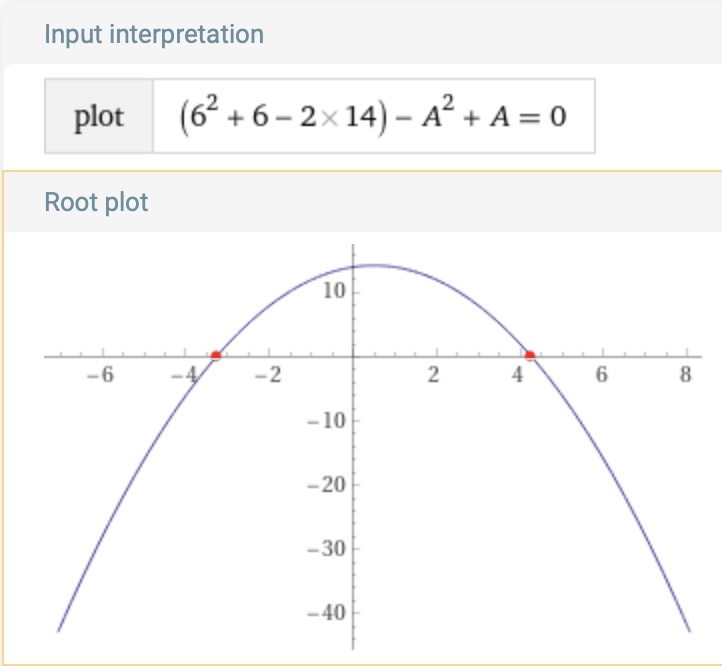
The positive root from the plot is about ~4.3. What this really means is that if we take the contiguous sum from 4.3 to \(N\) (\(N\) = 6) that would equal \(K\). But thats not legal is it?

So how we handle is, is to round it up to the nearest integer (5). Then, we need to realise that the remainder (~0.3) indicates that there is some number from 1 to int($$A$$) such that when it is added to the contiguous sum, we will get K!

What if the root is an integer value?

This happens when the contiguous sum from \(A\) to \(N\) is exactly equal to \(K\). Consider when \(K\) = 21 and \(N\) = 6.

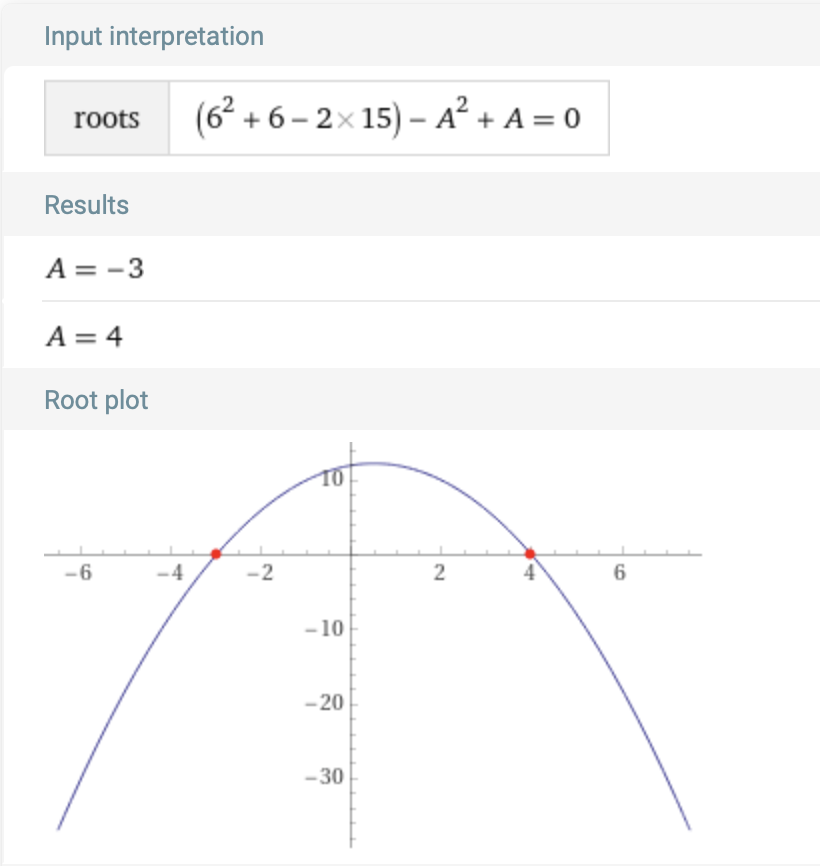
The positive root here is 4. This means that the sum from 4 to \(N\) (\(N\) = 6) is exactly \(K\).

All there is left to do is to properly handle cases where the positive root is a float and when it is an integer then count the number of integers needed to add to \(K\). This gives us an \(O(1)\) solution!

for those who are interested, there is a way to do this in O(log n) time. I will leave it as an exercise for the reader 😉.